洛谷 P1466 集合 Subset Sums Label：DP-白红宇

洛谷 P1466 集合 Subset Sums Label：DP

阅读量：7059 次

发布时间：2019-06-28

本文共 2316 字，大约阅读时间需要 7 分钟。

题目描述

对于从1到N (1 <= N <= 39) 的连续整数集合，能划分成两个子集合，且保证每个集合的数字和是相等的。举个例子，如果N=3，对于{1，2，3}能划分成两个子集合，每个子集合的所有数字和是相等的：

{3} 和 {1,2}

这是唯一一种分法（交换集合位置被认为是同一种划分方案，因此不会增加划分方案总数）如果N=7，有四种方法能划分集合{1，2，3，4，5，6，7}，每一种分法的子集合各数字和是相等的:

{1,6,7} 和 {2,3,4,5} {注 1+6+7=2+3+4+5}{2,5,7} 和 {1,3,4,6}{3,4,7} 和 {1,2,5,6}{1,2,4,7} 和 {3,5,6}给出N，你的程序应该输出划分方案总数，如果不存在这样的划分方案，则输出0。程序不能预存结果直接输出（不能打表）。

输入输出格式

输入格式：

输入文件只有一行，且只有一个整数N

输出格式：

输出划分方案总数，如果不存在则输出0。

输入输出样例

输入样例#1：

输出样例#1：

说明

翻译来自NOCOW

USACO 2.2

代码

1 #include
      
        2 #include
       
         3 #include
        
          4 #include
         
           5 #include
          
            6 #include
           
             7 using namespace std; 8 9 int f[100][1000];//f[i][j]表示i分成两组差为j的分法10 int N;11 12 int main(){13 // freopen("01.in","r",stdin);14 scanf("%d",&N);15 f[1][1]=f[2][3]=1;f[2][1]=1;16 for(int i=3;i<=N;i++){17 for(int j=0;j<=(i*(i+1)/2);j++){18 if(j+i<=(i*(i+1)/2)) f[i][j]+=f[i-1][j+i];19 if(j>=i) f[i][j]+=f[i-1][j-i];20 if(j!=0) f[i][j]+=f[i-1][i-j];21 }22 }23 24 printf("%d",f[N][0]);25 fclose(stdin);fclose(stdout);return 0;26 }

很明显这是一道DP，自己思考一下Line 18 19 20吧

转载另外一种解法：

题解by:redbag

原题解地址：

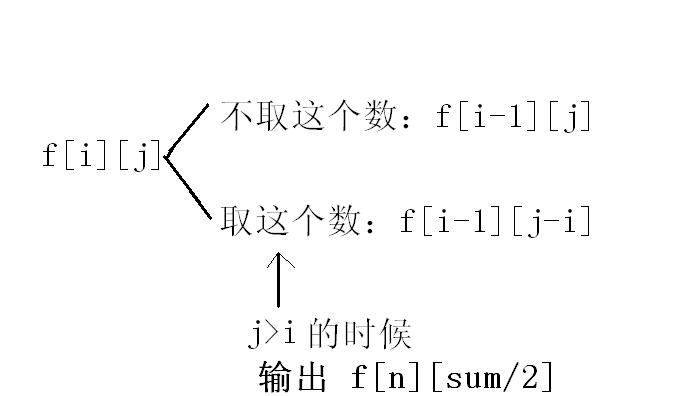
n个数的总和为sum:=n*(n+1)shr 1,当且仅当sum为偶数的时候才有解，sum为奇数时直接输出0并且退出程序；然后每个数只有2种情况，放在第一个集合和不放在第一个集合。于是就是简单的01背包问题了。简单的分析见图

1 #include
      
          2 #include
          3 #include
        
            4 #include
         
             5 #include
          
              6 #include
           
             7 #include
            
              8 #include
             
               9 #include
              
                10 #include
               
                 11 #include
                
                  12 #include
                 
                   13 #include
                  
                    14 #include
                   
                     15 #include
                    
                      16 #include
                     
                       17 #include
                      
                        18 #include
                       
                         19 #define LL unsigned long long 20 using namespace std;21 int sum/*1~n的和*/,n;22 int f[40][800];23 int i,j;24 int main() 25 {26 freopen("subset.in","r",stdin);27 freopen("subset.out","w",stdout); 28 scanf("%d",&n);29 sum=(n*(n+1))/2;//算出1~n的和。30 if (sum%2==1)//仅当sum为偶数的时候才有解 31 {32 printf("0\n");//因为分成的2份和要相等 33 return 0;34 } 35 f[1][1]=1;//1中取任意个数的数使和为1的情况36 f[1][0]=1;//1中取任意个数的数使和为0的情况 37 for (i=2;i<=n;i++)//1的情况已经算完了，所以从2开始 38 {39 for (j=0;j<=sum;j++)40 {41 if (j>i)//有取这个数和不取两种情况 42 f[i][j]=f[i-1][j]+f[i-1][j-i];43 else f[i][j]=f[i-1][j];//只能不取了44 }45 }46 printf("%d\n",f[n][sum/2]); 47 return 0;48 }

原来这只是一个辣么简单的背包，我想得。。。。。。。也太复杂了吧

转载于:https://www.cnblogs.com/radiumlrb/p/6059641.html

你可能感兴趣的文章